こんにちは、ナナです。
前回『Python set定義と追加・削除【順番のない情報を一括管理】』で紹介した『set』オブジェクトには、データを「集合」という形で制御するための機構が用意されています。
それでは「集合」とは何なのか、集合を操るための「集合演算」とは何なのか、を学んでいきましょう。
本記事では次の疑問点を解消する内容となっています。
では、『set』を使った「集合」と「集合演算」について学んでいきましょう。
setは「集合」を扱うオブジェクト

『set』というコンテナは、「集合」というデータを扱うためのオブジェクトなんですよね?「集合」っていうのは、結局なんなんですか?

学生の頃に数学の授業で「集合」というものを学んでいることでしょう。「そんなの習ったかな?」って人もいると思いますが、図を見れば「これか~」って思い出しますよ。
「集合」とは「ものの集まり」のことです。なんらかのグループに所属する「もの」を表したものです。
「集合」を思い出そう
皆さん、次のような図を学校で学んだ覚えはないですか?これが「集合」です。
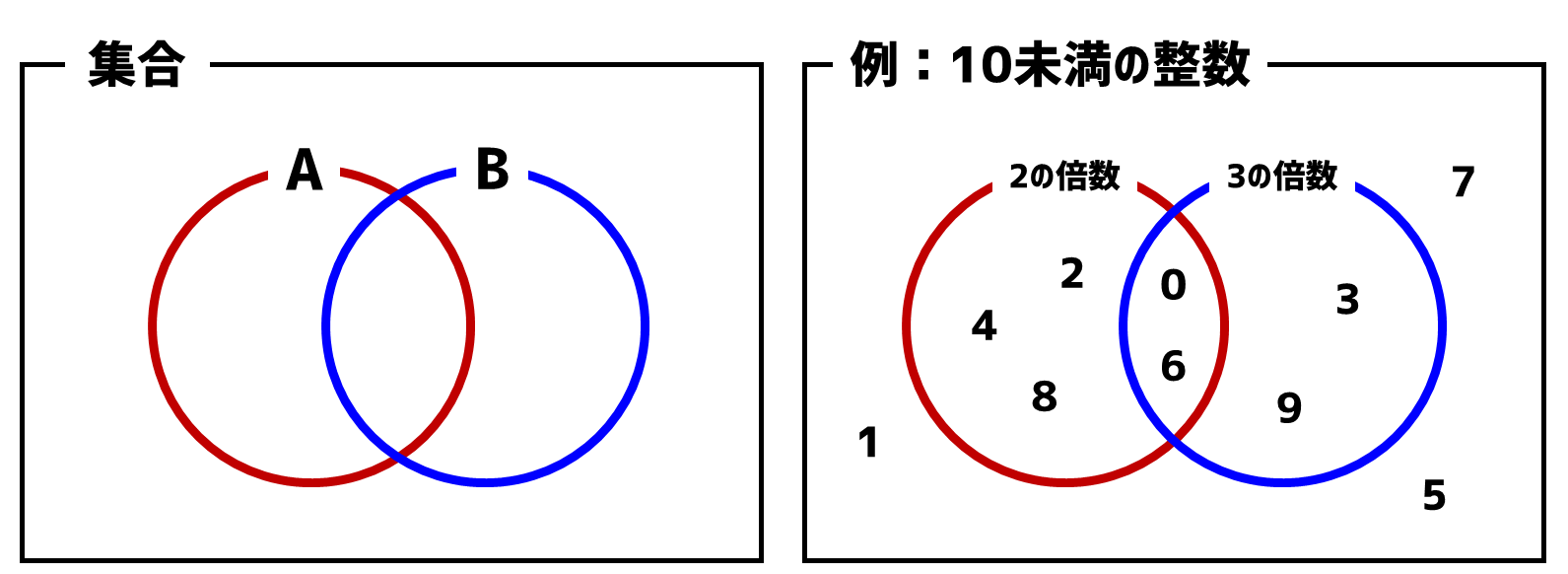
集合にはいくつかの種類があります。
それぞれの種類に応じて、異なる集合同士の関係性が次のように表現されます。
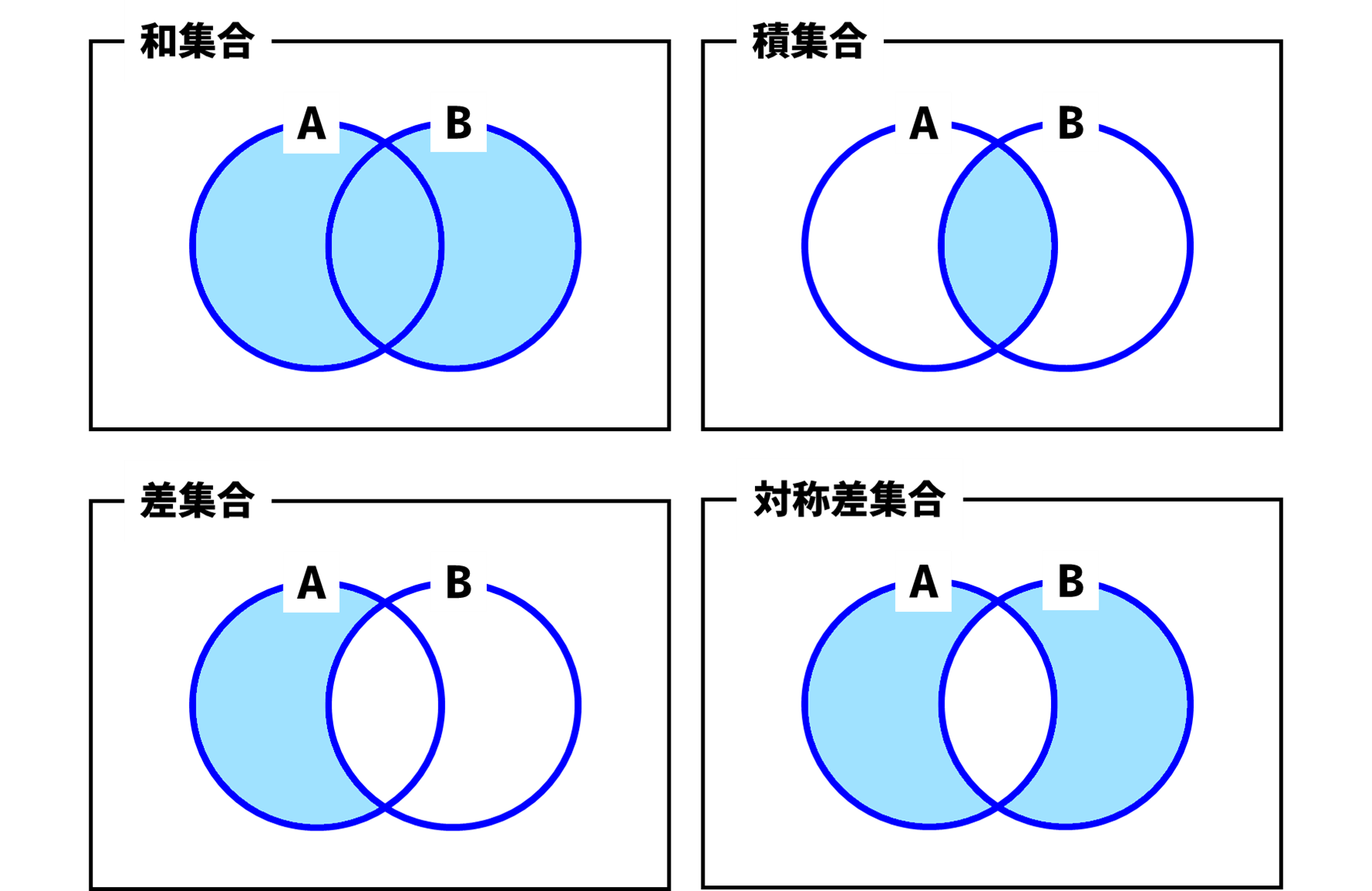
Pythonでは、これら集合の関係性を演算で簡単に作り出すことができます。この演算のことを「集合演算」と呼びます。

この「集合」の関係性を、プログラムから利用することができるのが『set』というコンテナなんです。
setオブジェクトの「集合演算」とは?
『set』オブジェクトには「集合演算」と呼ばれる演算を使うことができます。メソッド、もしくは演算子を使うことで、「和集合」などを表現することができるのです。
| 集合演算の種類 | メソッド名 | 演算子 | 抽出されるもの |
| 和集合 | union | | | 全てのもの |
| 積集合 | intersection | & | 共通のもの |
| 差集合 | difference | – | 片方のみのもの |
| 対称差集合 | symmetric_difference | ^ | 共通以外のもの |

目的に応じて集合演算を使い分ける必要があります。これから順に各集合演算の特徴を紹介しましょう!
setオブジェクトの集合演算を具体的な利用シーンで考える!

思い出しました、そうそう「集合」ってこんな種類があったんでしたね。でも、これをプログラムで使うってどういうことなんですか?
どうやって使うのか活用方法が全然ピンときません。

プログラムというのは「情報を如何に操るか」なんですよ。「集合」として管理された情報を、様々な集合演算で抽出して加工したりするんですよ。
それじゃあ、みんなにとって身近な「料理」を例に集合演算を使ってみようね
それでは、ここからは具体的な集合演算の使い方を学んでいきます。
料理のレシピから捉える「集合」の使い方
身近なものでも色々と使い道があるということを示すために、「料理」を題材に集合演算を学んでいきましょう。
今日と明日の晩御飯は「カレー」と「肉じゃが」にします。これらの料理を作るためにはもちろん具材が必要になりますね。

それでは次のように「カレー」と「肉じゃが」で使う具材を『set』オブジェクトで定義しておくとしましょう。
# setで「カレー」と「肉じゃが」の具材の定義
curry = {"ジャガイモ", "にんじん", "玉ねぎ", "豚肉", "カレー粉"}
nikujaga = {"ジャガイモ", "にんじん", "玉ねぎ", "牛肉", "しらたき", "さやえんどう"}この集合情報を利用して、必要な具材を買い物するシーンを想定しますよ!
setオブジェクト:和集合の使い方

「カレー」と「肉じゃが」を作るために必要な具材はわかってるんです。でも、同じ具材もあって結局、何が必要なのかまとめられないんです。
全部の具材がまとまったリストが欲しいんです。えーん(泣)。

そんな時に使うのが「和集合」だよ。和集合を使えば全ての具材を重複なしに抽出することができるんだよ!
和集合は2つのグループを合わせた情報を抽出することができます。
和集合を使ったプログラム
今回は「カレー」と「肉じゃが」で必要な具材を全て洗い出せるようにしましょう。
# 「カレー」と「肉じゃが」の具材の定義
curry = {"カレー粉", "にんじん", "ジャガイモ", "玉ねぎ", "豚肉"}
nikujaga = {"ジャガイモ", "玉ねぎ", "牛肉", "しらたき", "さやえんどう"}
# 「和集合」で全ての具材を抽出
shopping = curry | nikujaga
# 抽出した具材を表示
print(shopping){'玉ねぎ', 'ジャガイモ', 'しらたき', 'カレー粉', 'にんじん', 'さやえんどう', '豚肉', '牛肉'}「和集合」を実施すると、「カレー」と「肉じゃが」で必要な具材が全て抽出できましたね。具材がもっと多くても、和集合を利用すれば漏れも重複もなく洗い出すことができます。
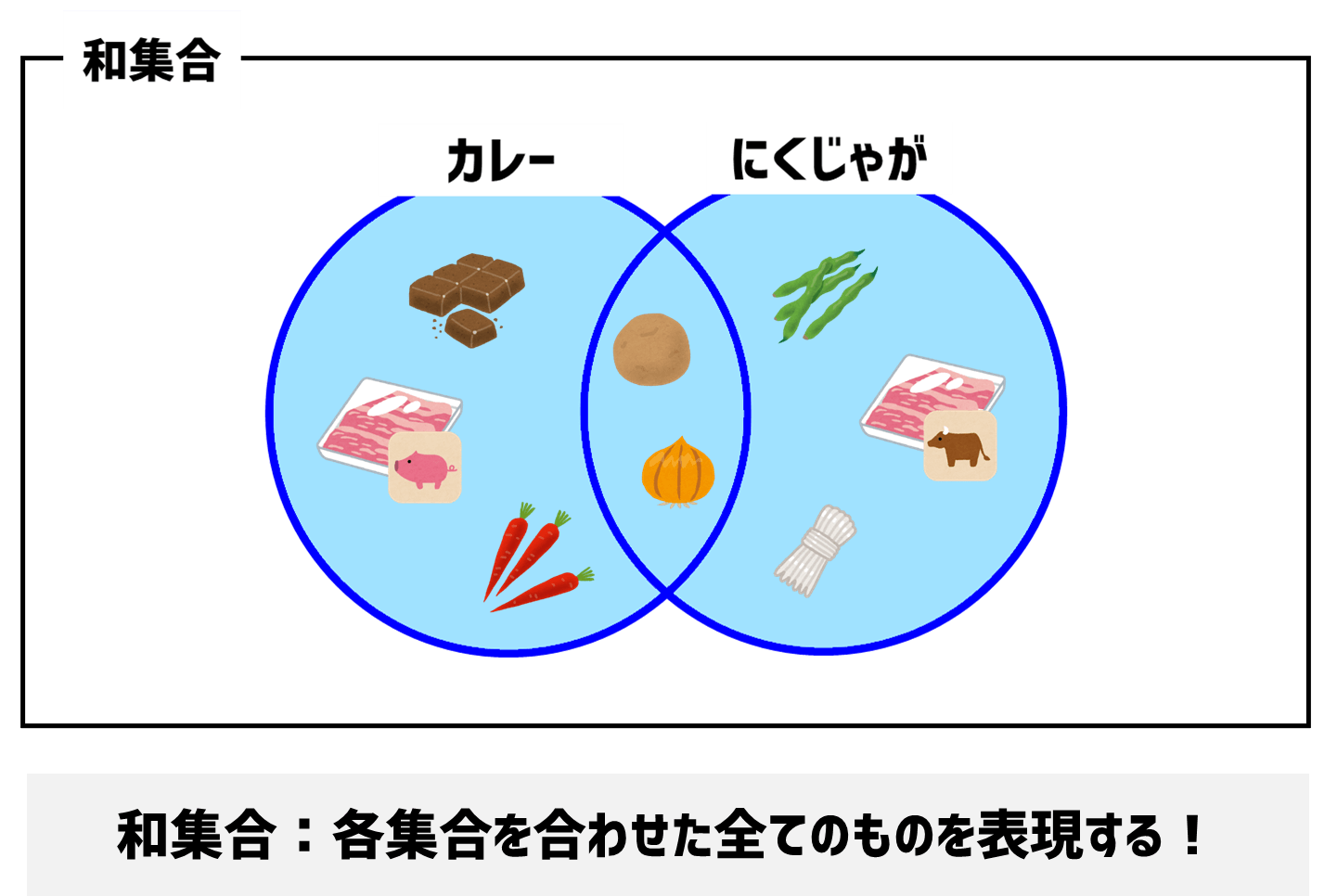
集合には演算子を使っても、メソッドを使っても同様の結果が得られます。
# 「和集合」で全ての具材を抽出
shopping = curry | nikujaga # 演算子
shopping = curry.union(nikujaga) # メソッド
「和集合」で具材のリストが手に入ったわ!このリストで買い物すれば、忘れ物がないわね。
setオブジェクト:積集合の使い方

具材のリストは手に入ったんですけど、よく考えると「カレー」と「肉じゃが」で両方使う具材があるんです。その具材って多めに買っておかないといけないんです。
「カレー」と「肉じゃが」の両方で使う具材が知りたいんです!

なるほど、そんな時に使うのは「積集合」だね。これを使うと、集合同士で共通するものを抽出することができるんだよ!
積集合を使ったプログラム
今回は「カレー」と「肉じゃが」で共通する具材を洗い出せるようにしましょう。
# 「カレー」と「肉じゃが」の具材の定義
curry = {"カレー粉", "にんじん", "ジャガイモ", "玉ねぎ", "豚肉"}
nikujaga = {"ジャガイモ", "玉ねぎ", "牛肉", "しらたき", "さやえんどう"}
# 「積集合」で共通する具材を抽出
shopping = curry & nikujaga
# 抽出した具材を表示
print(shopping){'玉ねぎ', 'ジャガイモ'}「積集合」を実施すると、「カレー」と「肉じゃが」の両方で必要な具材が抽出できましたね。
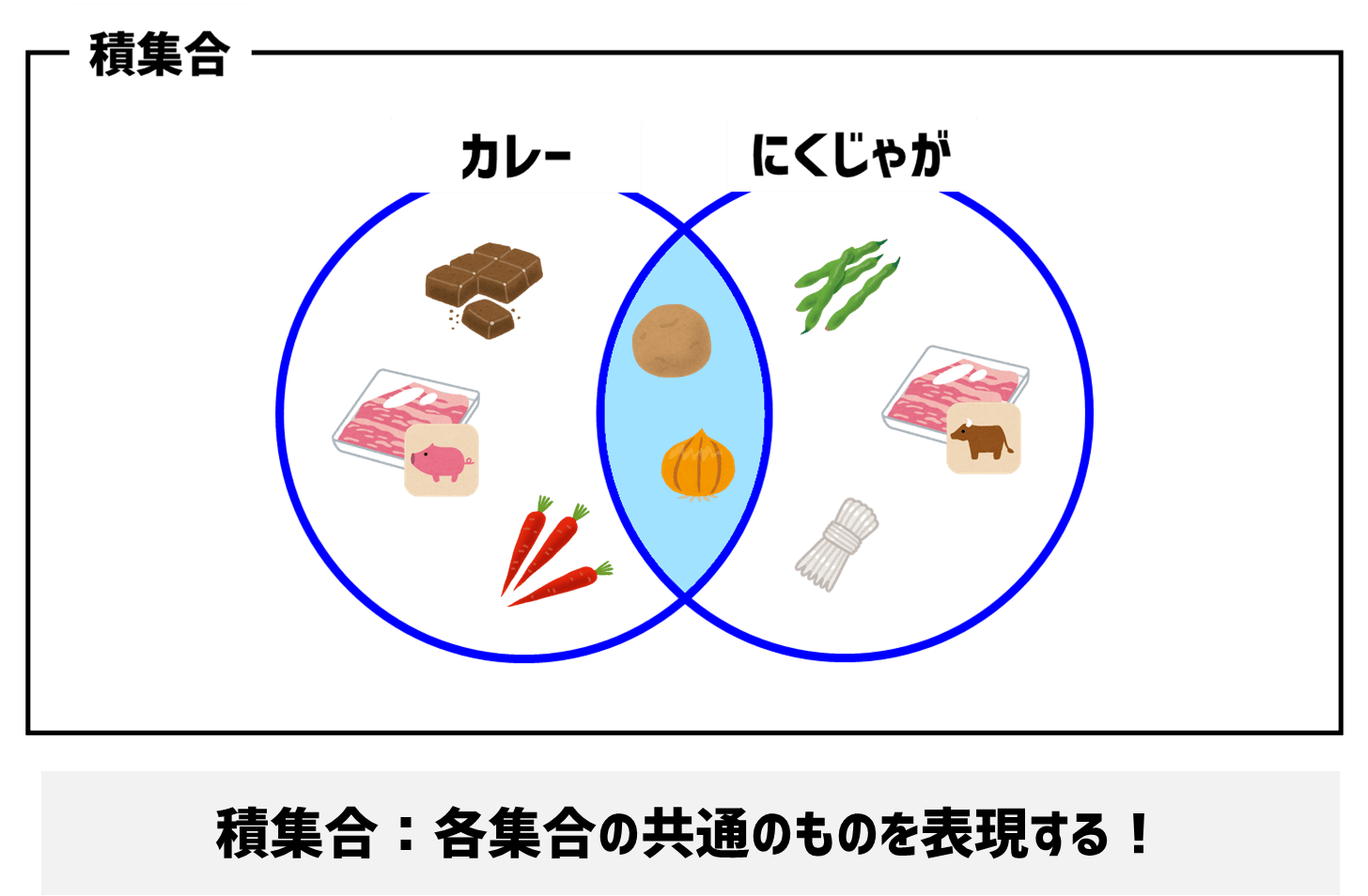
集合には演算子を使っても、メソッドを使っても同様の結果が得られます。
# 「積集合」で共通する具材を抽出
shopping = curry & nikujaga # 演算子
shopping = curry.intersection(nikujaga) # メソッド
そっかー、「じゃがいも」と「玉ねぎ」を多めに買っておこう!「積集合」ってこんな風に役立つのね。
setオブジェクト:差集合の使い方

「カレー」をみんなにふるまったら、大好評で具材がたりなくなっちゃったんです。
「肉じゃが」の具材は残ってるんですけど、「カレー」だけで使う具材ってなんだったかな?

なるほど、そんな時に使うのは「差集合」だね。これを使うと、集合同士の差で片方の集合のにあるものを抽出することができるんだよ!
差集合を使ったプログラム
今回は「カレー」のみで使われる具材を洗い出せるようにしましょう。
# 「カレー」と「肉じゃが」の具材の定義
curry = {"カレー粉", "にんじん", "ジャガイモ", "玉ねぎ", "豚肉"}
nikujaga = {"ジャガイモ", "玉ねぎ", "牛肉", "しらたき", "さやえんどう"}
# 「差集合」で「カレー」のみの具材を抽出
shopping = curry - nikujaga
# 抽出した具材を表示
print(shopping){'にんじん', '豚肉', 'カレー粉'}「差集合」を実施すると、「カレー」のみで必要な具材が抽出できましたね。
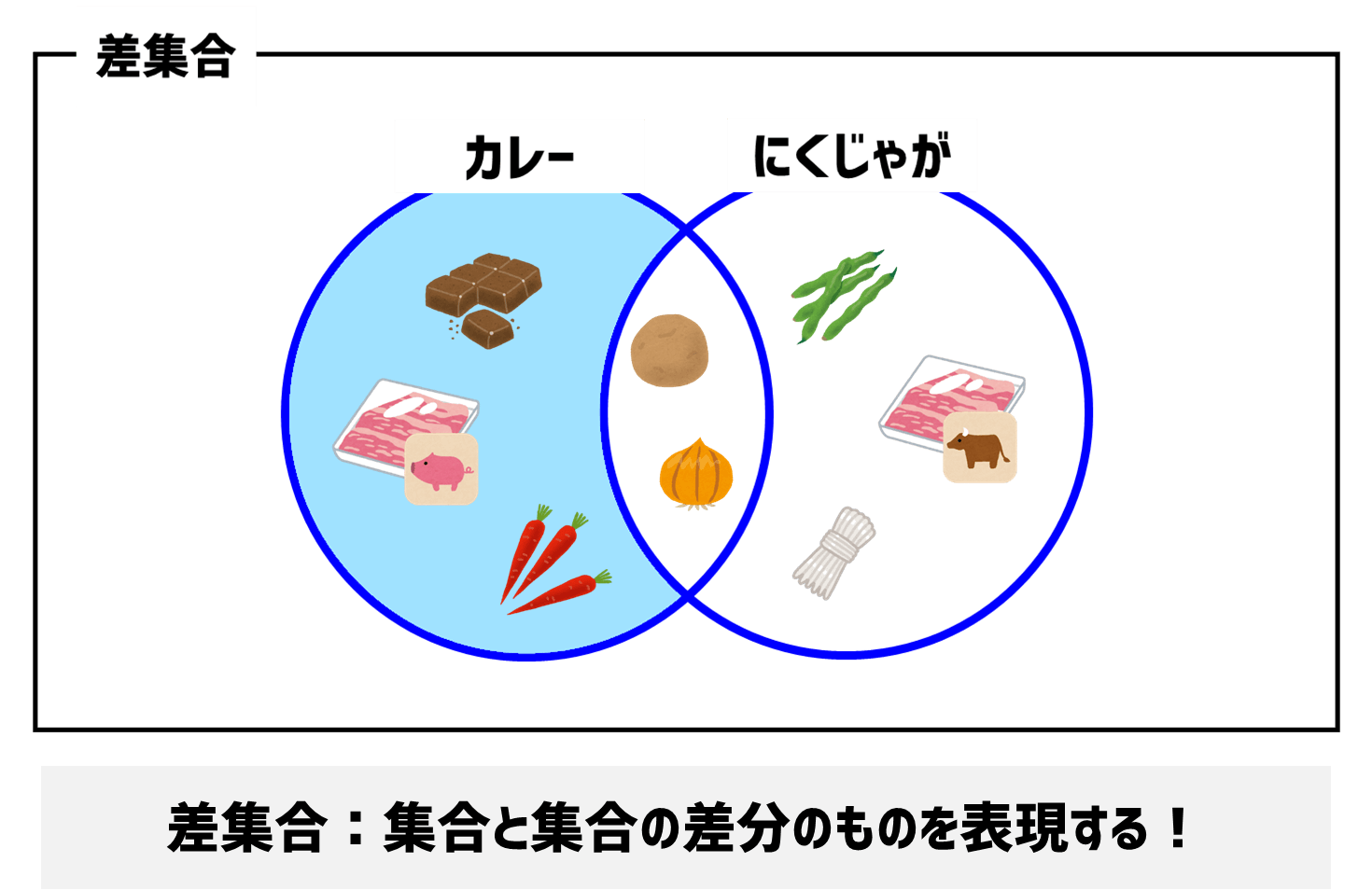
集合には演算子を使っても、メソッドを使っても同様の結果が得られます。
# 「差集合」で「カレー」のみの具材を抽出
shopping = curry - nikujaga
shopping = curry.difference(nikujaga)
カレーだけに必要なのは「カレー粉」と「人参」と「豚肉」ね。みんなのために、買ってこなくっちゃ!
setオブジェクト:対称差集合の使い方

「積集合」で共通する具材は洗い出せましたけど、逆に「カレー」と「肉じゃが」でしか使わない具材は少なめの購入でいいんです。
このリストを手に入れることはできないですか?

ふむ、そんな時に使うのは「対称差集合」だね。これを使うと、集合同士で共通しないものを抽出することができるんだよ!
この「対称差集合」は「排他的論理和」とも呼ばれます。
対称差集合を使ったプログラム
「カレー」と「肉じゃが」で共通しない具材を洗い出せるようにしましょう。
# 「カレー」と「肉じゃが」の具材の定義
curry = {"カレー粉", "にんじん", "ジャガイモ", "玉ねぎ", "豚肉"}
nikujaga = {"ジャガイモ", "玉ねぎ", "牛肉", "しらたき", "さやえんどう"}
# 「対称差集合」で共通する具材を抽出
shopping = curry ^ nikujaga
# 抽出した具材を表示
print(shopping){'カレー粉', '牛肉', '豚肉', 'にんじん', 'しらたき', 'さやえんどう'}「対称差集合」を実施すると、「カレー」と「肉じゃが」で共通しない具材が抽出できましたね。
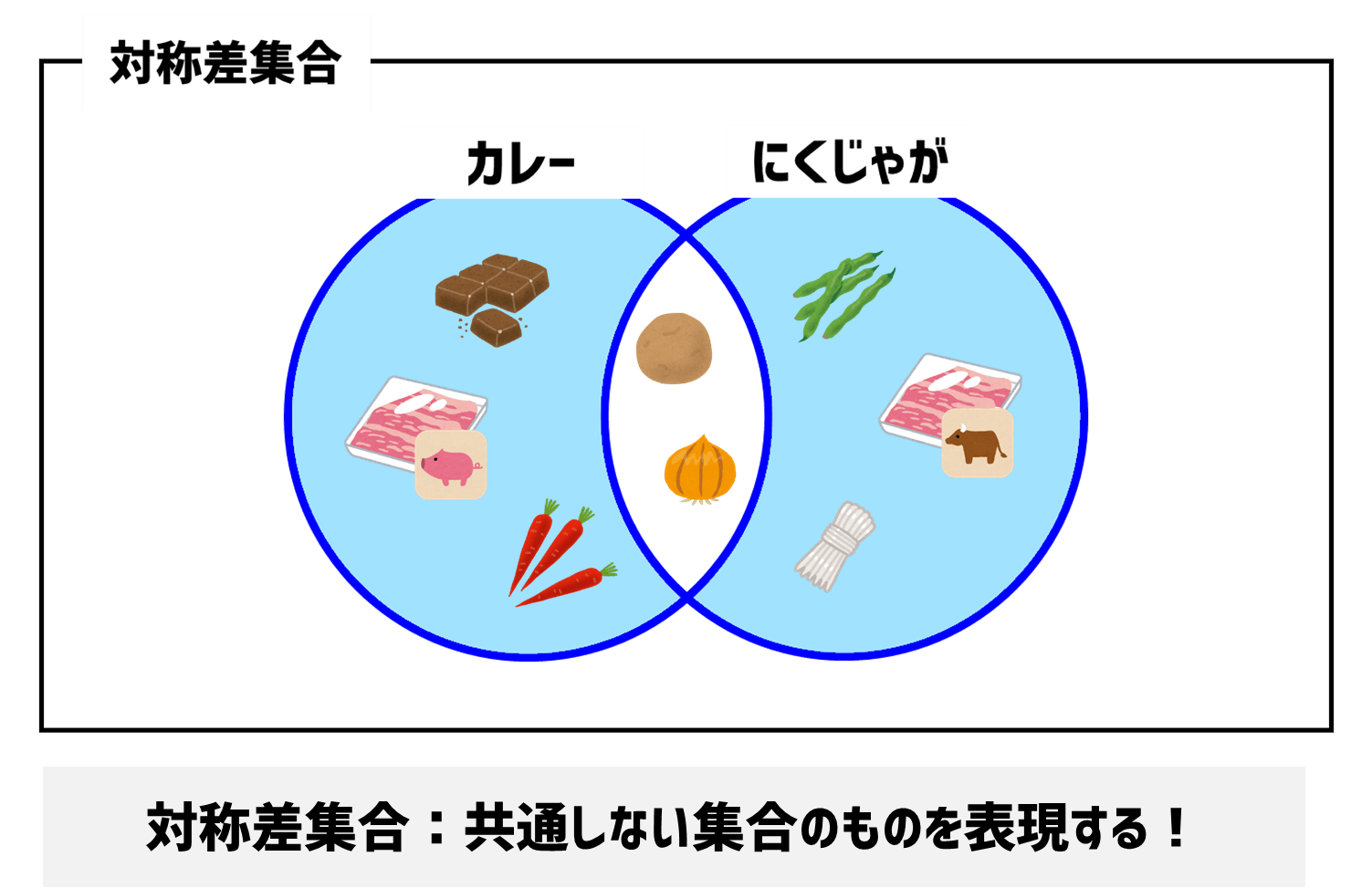
集合には演算子を使っても、メソッドを使っても同様の結果が得られます。
# 「対称差集合」で共通する具材を抽出
shopping = curry ^ nikujaga
shopping = curry.symmetric_difference(nikujaga)
よーし、これらの具材は少し買えばOKね。無駄に買わずにすんだわ!
Q&A:集合演算に関するよくある質問

集合演算で何か質問ある人はどうぞ!
Q:集合演算は演算子とメソッドがあるけど、どっちを使うのがいいの?

集合演算を使うときって、演算子でもメソッドでも使えますね。例えば「和集合」を使う時は「OR演算子」と「unionメソッド」の両方が使えるじゃないですか。
これって効果は同じなんですよね。どっちを使うのがいいんですか?

慣れていると演算子の場合の方が直感的でわかりやすいですね。集合が3つ以上の場合でも自然な書き方ができますよ。
それでは、「すき焼き」のメニューを追加してみましょう。演算子による「和演算」は次のように自然な形で表現することができます。
# 「カレー」と「肉じゃが」と「すき焼き」の具材の定義
curry = {"カレー粉", "にんじん", "ジャガイモ", "玉ねぎ", "豚肉"}
nikujaga = {"ジャガイモ", "玉ねぎ", "牛肉", "しらたき", "さやえんどう"}
sukiyaki = {"牛肉", "長ねぎ", "しめじ", "豆腐", "糸こんにゃく"}
# 演算子による「和集合」
shopping = curry | nikujaga | sukiyaki
# 抽出した具材を表示
print(shopping){'さやえんどう', '豚肉', 'にんじん', '豆腐', 'ジャガイモ', 'しらたき', '長ねぎ', 'カレー粉', '玉ねぎ', 'しめじ', '糸こんにゃく', '牛肉'}それでは、「unionメソッド」を使った場合も紹介しましょう。いくつか書き方はありますが、次のようなプログラムになります。
# 「カレー」と「肉じゃが」と「すき焼き」の具材の定義
curry = {"カレー粉", "にんじん", "ジャガイモ", "玉ねぎ", "豚肉"}
nikujaga = {"ジャガイモ", "玉ねぎ", "牛肉", "しらたき", "さやえんどう"}
sukiyaki = {"牛肉", "長ねぎ", "しめじ", "豆腐", "糸こんにゃく"}
# unionメソッドによる「和集合」
shopping = curry.union(nikujaga).union(sukiyaki) # 書き方1
shopping = curry.union(nikujaga.union(sukiyaki)) # 書き方2
# 抽出した具材を表示
print(shopping)少し違和感のあるプログラムになっていますね。

集合演算は、演算子による書き方に慣れておくとよいでしょう!

Python言語を最初から学びたい人は、こちらの記事から順に始めましょう!








